[扩展] 四个电阻有多少种不同的连接方式?
在之前的微信推文(点击跳转)中,我们分享了 美国物理教师 2023 年 12 月杂志上刊登的一个问题:
有四个电阻,阻值分别为
文章给出了三个不同电阻共有 4 种排列方式,共计 8 种不同的总阻值。
那么,文章给出的答案是否是唯一的?以及,4个不同电阻的阻值有多少种排列方式,以及有多少种不同的总阻值,让我们来一探究竟。
可能会有不详尽的地方,还请批评指正。
如果四个电阻均相等...
我们可以从最简单的情况出发,假定四个电阻均为
可以试着组合下,只要学过一点电路的串并联知识,总能命中集中排列吧
让我们来揭示答案吧,总阻值共有 9 个!
阻值分别为:
我也在一篇文章找到了说法:
Sameen Ahmed Khan. The bounds of the set of equivalent resistances of n equal resistors combined in series and in parallel. https://doi.org/10.48550/arXiv.1004.3346, 2010

原文:We continue the exercise with 4 resistors and find 9 equivalent resistances, but ten different configurations. The following two configurations have the same equivalent resistance. 译文:我们继续研究 4 个电阻的情况,共有 9 个等效电阻,但有10 种构型,下图的两种构型有相同的等效电阻。
从这张表格,确实发现了存在 10 种构型,第 5 种构型和第 6 种构型的等效电阻均为
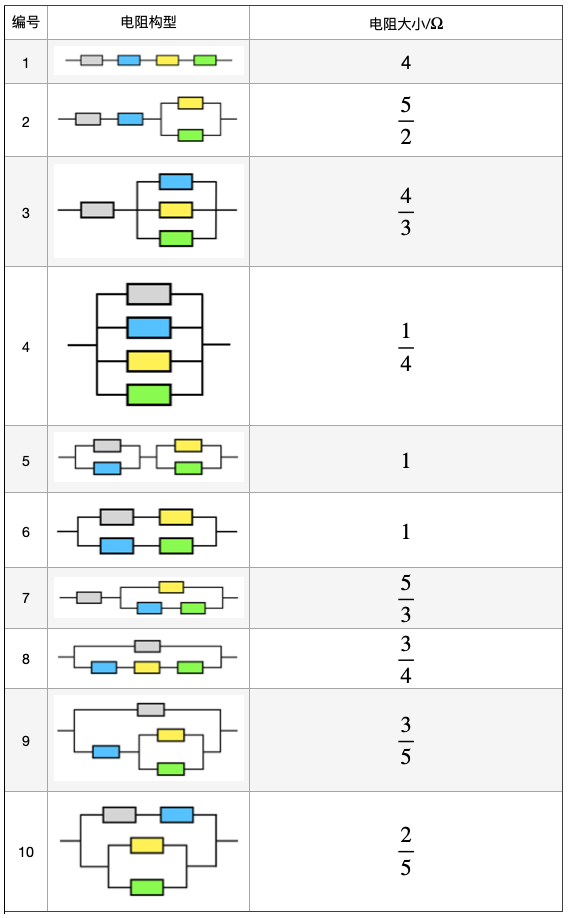
四个电阻为
那如果四个电阻分别为
我用 Mathematica 软件验证了情况,共有 48 种等效电阻值,如下所示 (真的很多!眼睛都要花了)
如有遗留,还请指正。
从上面的数据而言,四个电阻为
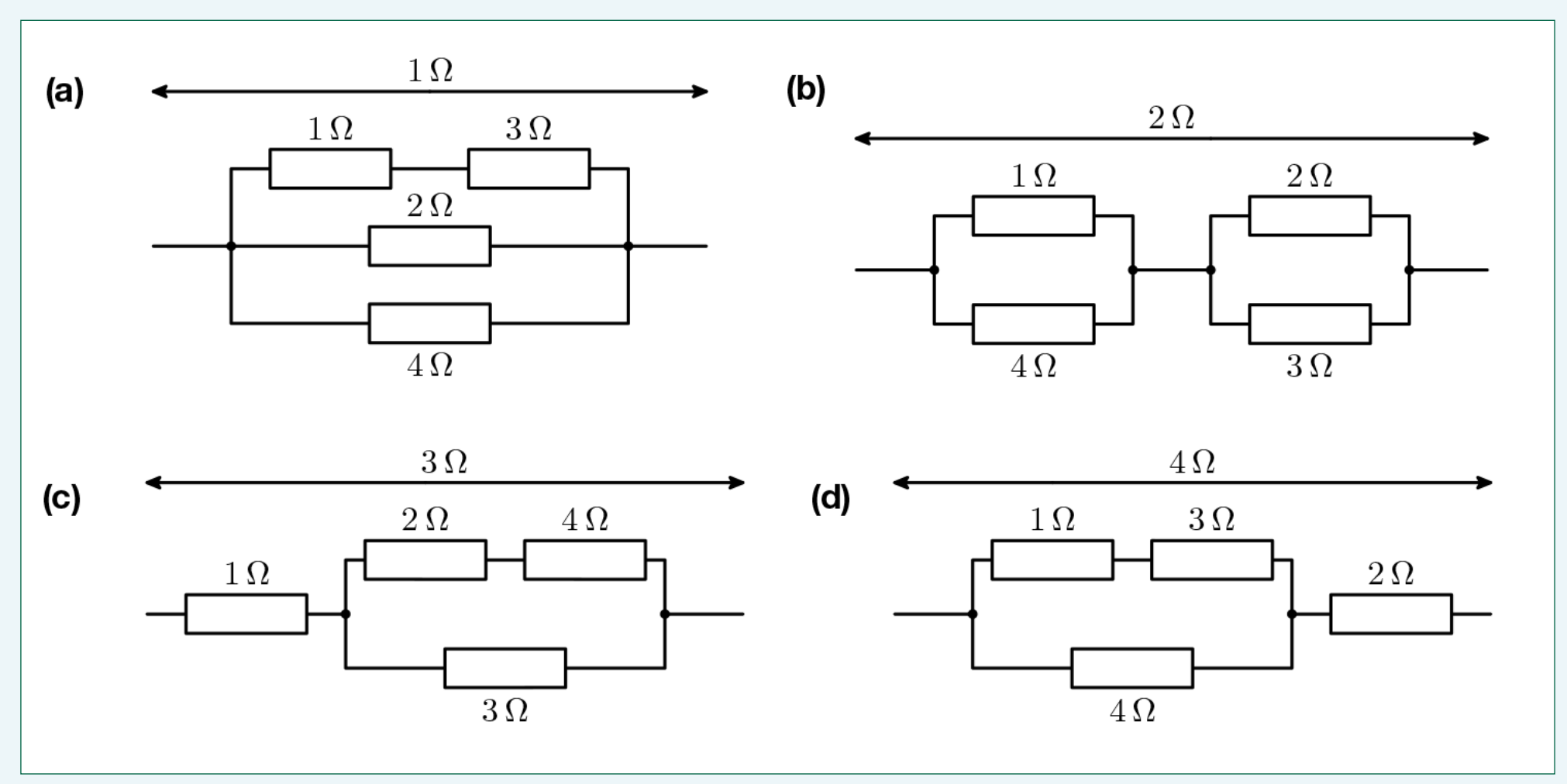
更一般的情况...
好吧,手动排了一下4个不同阻值的电阻,共有多少种可能的等效电阻。
共有 10 种构型,不同总电阻有 52 种!如下图所示
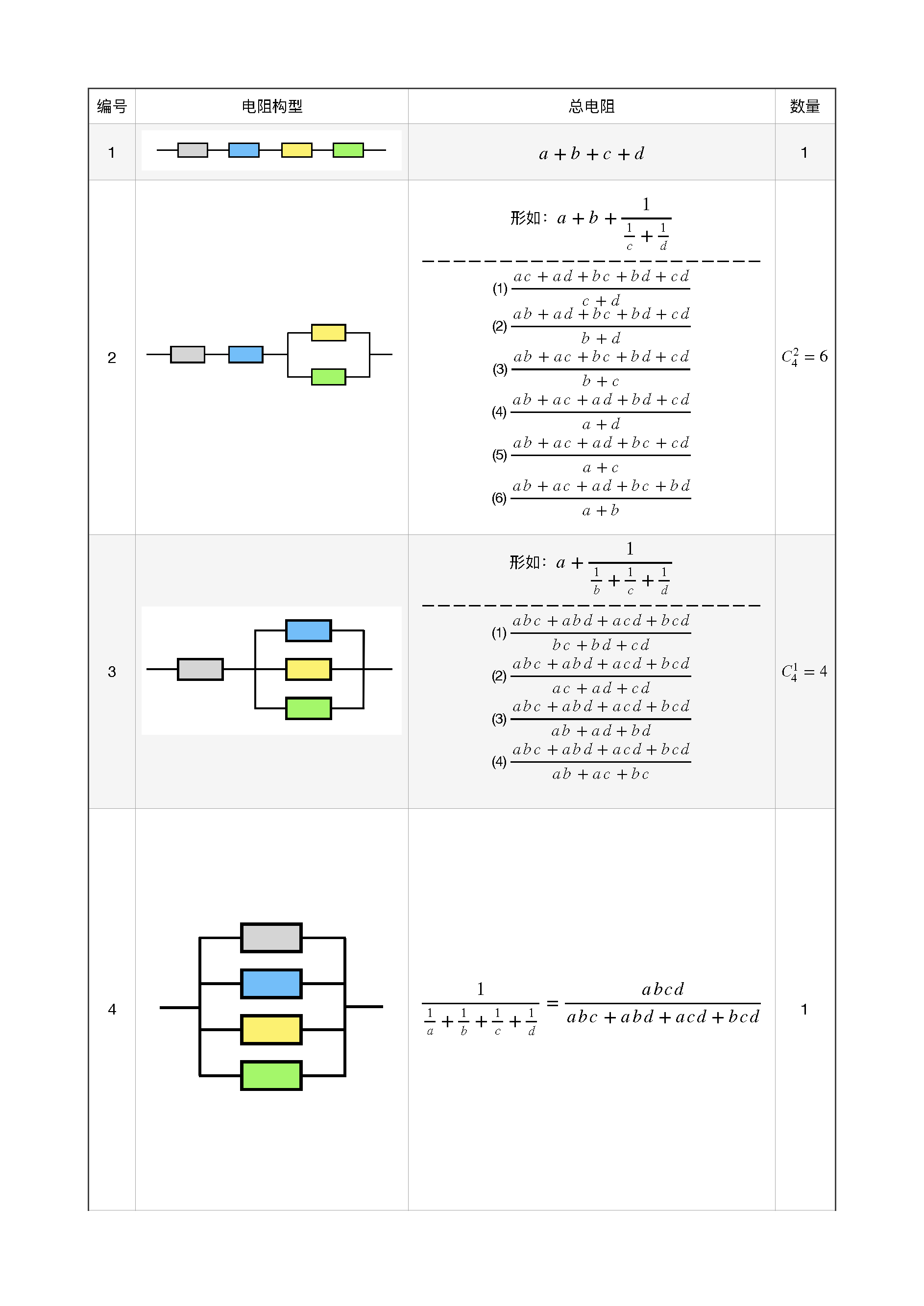
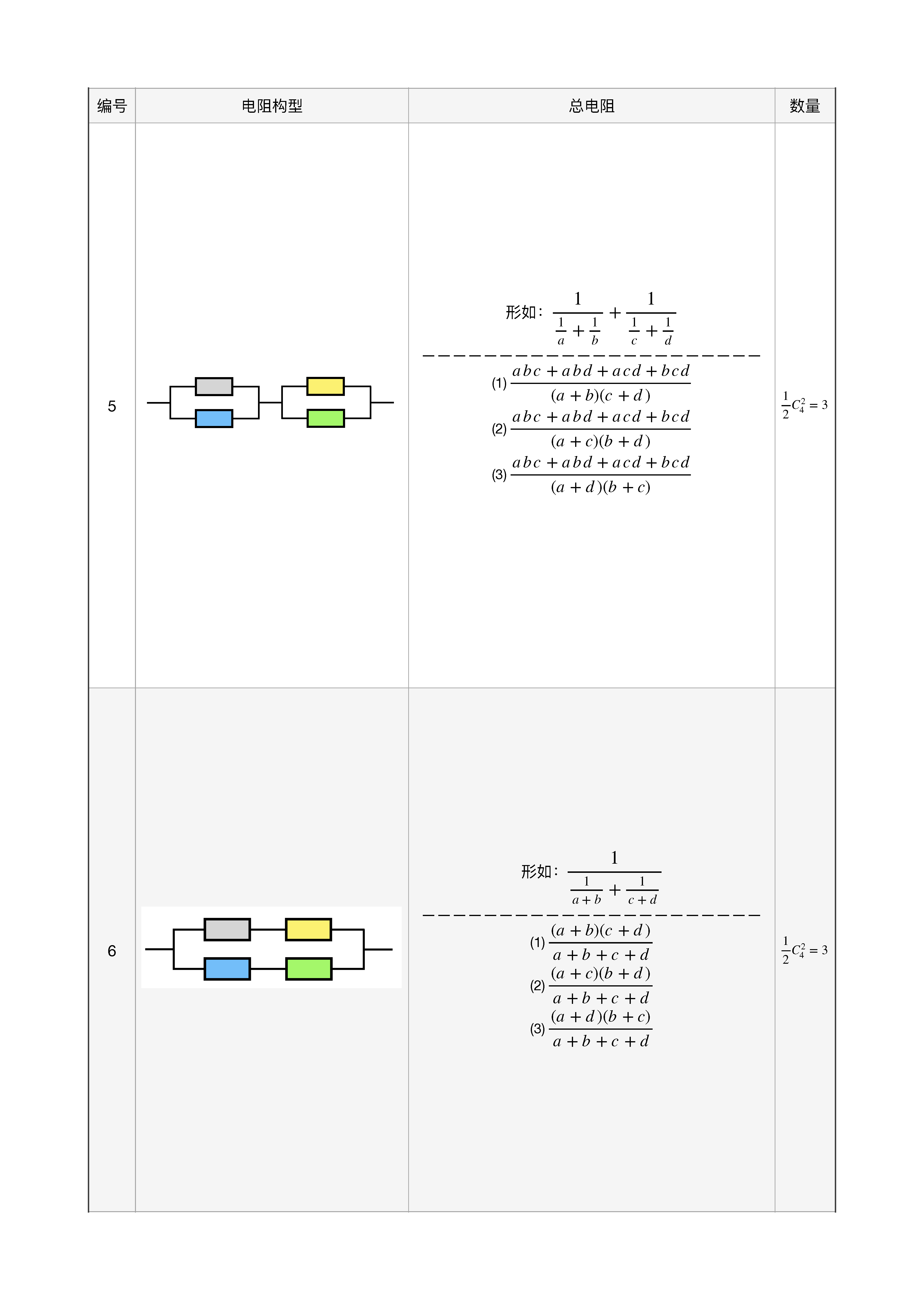
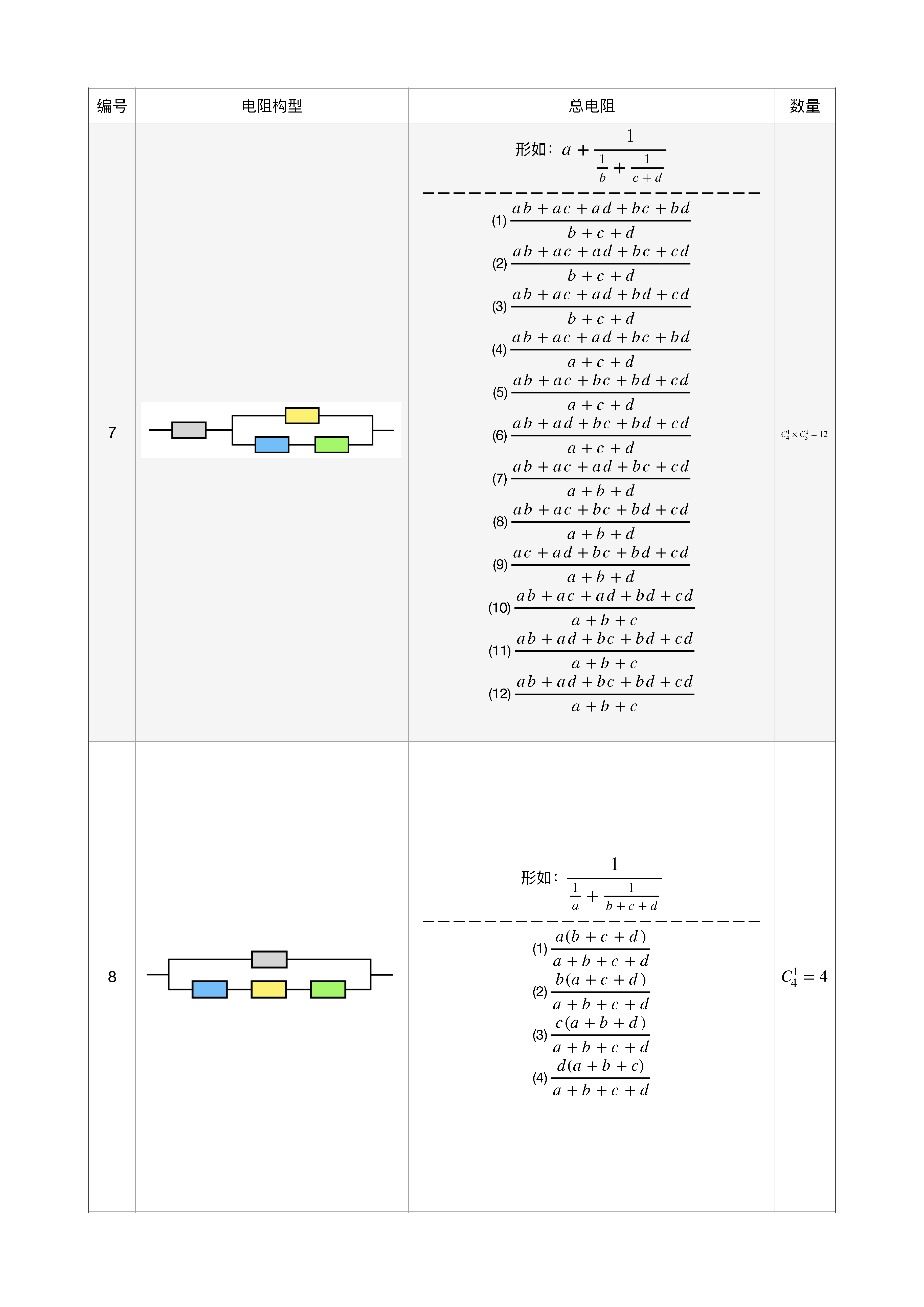
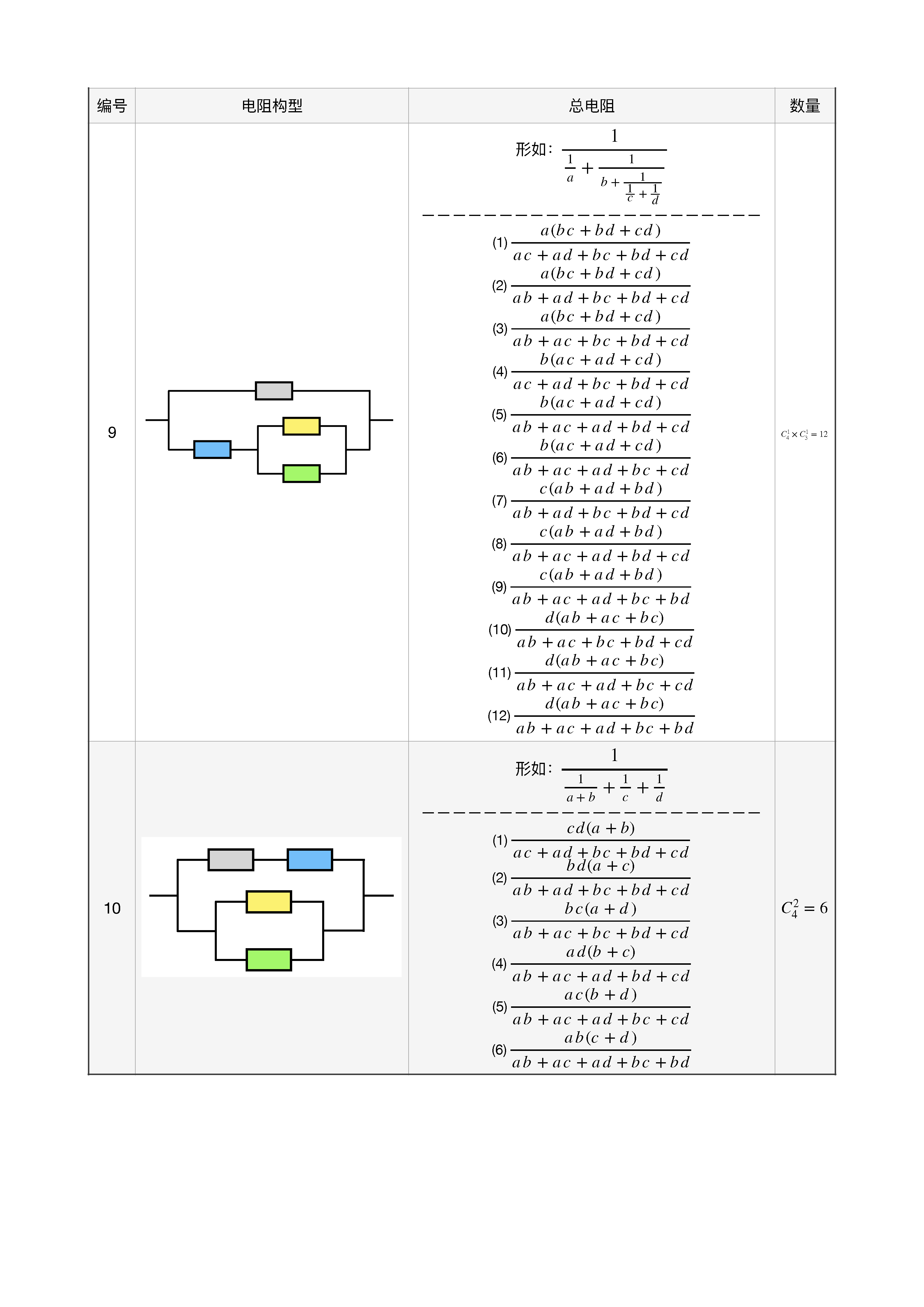
好了,本文就到这里。
致谢:Powered by Mathematica. 上图的电阻化简和计算阻值均来自 Mathematica 软件。
如有遗漏欢迎指正。
「物理说」公众号回复 "4ResistorCombination" 即可获得 Mathematica 程序。