[扩展] 车轮上飞溅出的雨滴最远能到哪-2

之前的微信推文中 提到了一个问题：车轮上飞溅出的雨滴最远能到哪？将这问题简化如下：

一个车轮绕固定点 $O$ 做匀速圆周运动。某一时刻，车轮上的一质量为 $m$ 的水滴以速度 $v_0$ 从车轮上飞出，并最终落到地面上的 $L$ 点。假设$O$ 点下方对应地面上的点为 $O^{\prime }$。当水滴从竖直方向转过 $\theta$ 角飞出，此时 $O^{\prime }L$ 的距离最大。求转过角度 $\theta$，以及最远距离$O^{\prime }{L}_{max}$？

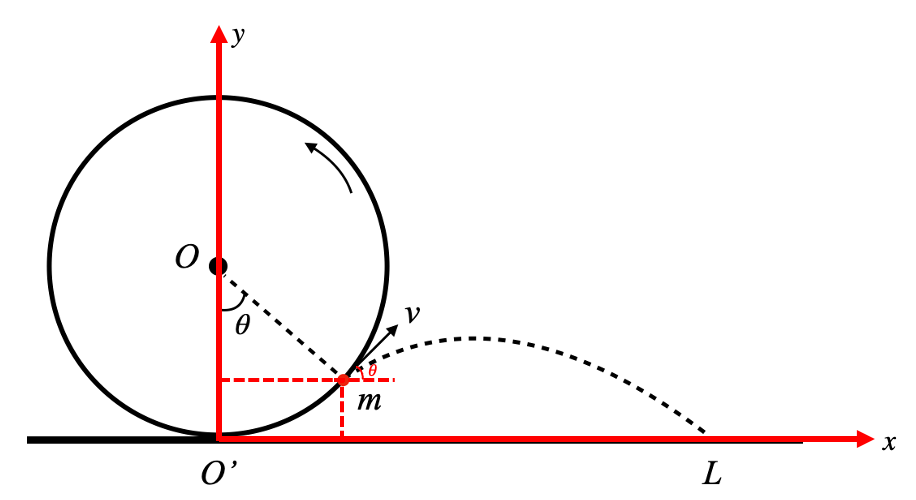
之前用 GeoGebra 做了个简单的演示。

视频可在微信公众号「物理说」上查看

---

这篇文章来(更数学地)分析下水滴抛出的距离。

首先建立坐标轴$O‘-xy$，则水滴抛出点的坐标为 $(Rsin\theta ,R-Rcos\theta )$。记水滴飞溅时刻为 $t=0$，不考虑空气阻力等因素，则水滴经过 $t$ 时间后水平方向位移为：

$$x=Rsin\theta +v_{0}cos\theta t$$

竖直方向位移为

$$y=R-Rcos\theta +v_{0}sin\theta t-\frac{1}{2}g{t}^2$$

当水滴到地面时，满足 $y=0$，则可以计算出水滴在空中飞行时间 $t_{max}$，从而得到水平方向的位移。

使用 Mathematica 软件，可以得到水滴飞溅时间为

$$t_{max}=\frac{v_{0}sin\theta +\sqrt{2g(R-Rcos\theta +v_0^{2}si{n}^2\theta )}}{g}$$

代入得到水平方向位移 $L$

$$L=Rsin\theta +v_{0}cos\times \frac{v_{0}sin\theta +\sqrt{2g(R-Rcos\theta +v_0^{2}si{n}^2\theta )}}{g}$$

水平方向位移$L$ 是$\theta$ 的函数，当 $\theta$ 满足 ${\theta }_0$ 时，能使得 $L$ 最大，即求 $\frac{dL}{d\theta }=0$，并讨论两侧导数的正负号，从而判断当 $\theta ={\theta }_0$ 时，$L$ 能否取到最大值。

这里的计算过程比较复杂，有兴趣的朋友可自行计算。

这里绘制了当 $R=0.3m$，$g=10N/kg$，$v_0=1m/s$ 条件下，飞溅落地距离 $L$ 和 $\theta$ 的关系图。

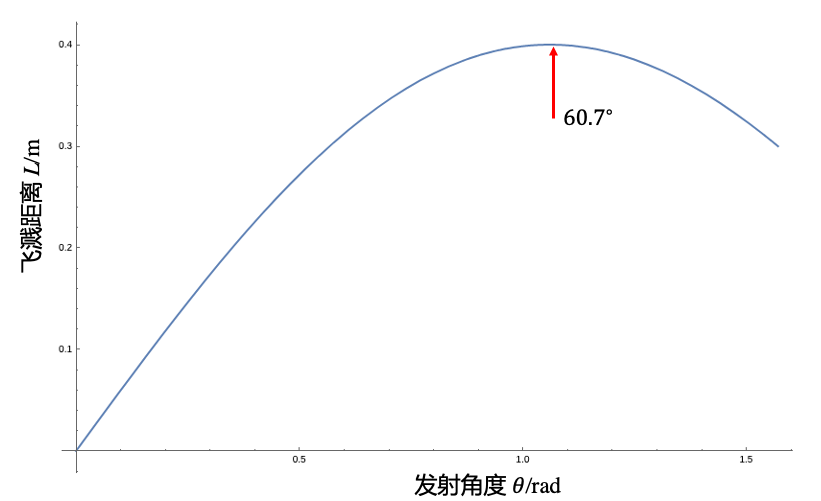
在 $\theta ={60.7}^{\circ }$ 时，飞溅最远距离为 $L_{max}=0.4m$。

---

致谢：感谢 Mathematica 软件提供支持。